noojennaka: จำนวนเชิงซ้อน

จำนวนเชิงซ้อน (อังกฤษ : complex number) ในทางคณิตศาสตร์ คือ เซตที่ต่อเติมจากเซตของจำนวนจริงโดยเพิ่มจำนวน

i

ซึ่งทำให้สมการ

i 2 + 1 = 0

เป็นจริง และหลังจากนั้นเพิ่มสมาชิกตัวอื่นๆ เข้าไปจนกระทั่งเซตที่ได้ใหม่มีสมบัติปิดภายใต้การบวกและการคูณ จำนวนเชิงซ้อน

z

ทุกตัวสามารถเขียนอยู่ในรูป

x + i y

โดยที่

x

และ

y

เป็นจำนวนจริง โดยเราเรียก

x

และ

y

ว่าส่วนจริง (real part) และส่วนจินตภาพ (imaginary part) ของ

z

ตามลำดับ
เซตของจำนวนเชิงซ้อนทุกตัวมักถูกแทนด้วยสัญลักษณ์ $\mathbb{C}$ จากนิยามข้างต้นเราได้ว่าเซตของจำนวนจริงเป็นสับเซตของเซตของจำนวนเชิงซ้อน ดังนั้นจำนวนจริงทุกตัวเป็นจำนวนเชิงซ้อน เราสามารถบวก ลบ คูณ และหารสมาชิกสองตัวใดๆ ของเซตของจำนวนเชิงซ้อนได้ (เว้นแต่ในกรณีที่ตัวหารคือศูนย์) และผลลัพธ์ที่ได้จำเป็นจำนวนเชิงซ้อนเสมอ ดังนั้นในทางคณิตศาสตร์เราจึงกล่าวว่าเซตของจำนวนเชิงซ้อนเป็นฟีลด์ นอกจากนี้เซตของจำนวนเชิงซ้อนยังมีสมบัติปิดทางพีชคณิต (algebraically closed) กล่าวคือ พหุนามที่มีสัมประสิทธิ์เป็นจำนวนเชิงซ้อนจะมีราก (พหุนาม)เป็นจำนวนเชิงซ้อนด้วย สมบัตินี้เป็นที่รู้จักในชื่อทฤษฎีบทมูลฐานของพีชคณิต
นอกจากนี้ ในทางคณิตศาสตร์แล้วคำว่า "เชิงซ้อน" ถูกใช้เป็นคำคุณศัพท์ที่มีความหมายว่าฟีลด์ของตัวเลขที่เราสนใจคือฟีลด์ของจำนวนเชิงซ้อน ยกตัวอย่างเช่น การวิเคราะห์เชิงซ้อน, พหุนามเชิงซ้อน, แมทริกซ์เชิงซ้อน, และพีชคณิตลีเชิงซ้อน เป็นต้น
นิยาม

ฟีลด์ของจำนวนเชิงซ้อน

ฟีลด์ของจำนวนเชิงซ้อน $\mathbb{C}$ ประกอบด้วยเซตของคู่ลำดับ

(a, b)

ทั้งหมดโดยที่

a

และ

b

เป็นจำนวนจริง และปฏิบัติการสองตัวคือ

+

(การบวก) และ $\cdot$ (การคูณ) โดยปฏิบัติการทั้งมีนิยามดังต่อไปนี้
ให้

(a, b)

และ

(c, d)

เป็นจำนวนเชิงซ้อนใดๆ

$(a,b)+(c,d) = (a+c, b+d) \,$

$(a,b)\cdot(c,d) = (ac-bd, ad+bc) \,$

เมื่อการบวก การลบ และการคูณภายในคู่ลำดับคือการบวก การลบ และการคูณจำนวนจริง
เซตของจำนวนเชิงซ้อนและปฏิบัติการทั้งสองมีสมบัติเป็นฟีลด์ กล่าวคือ

การบวกและการคูณมีสมบัติปิด การสลับที่ การเปลี่ยนกลุ่ม และการแจกแจง
มีเอกลักษณ์การบวกคือ $(0,0)$
มีเอกลักษณ์การคูณคือ $(1,0)$
อินเวอร์สการบวกของ $z = (a, b)$ (เขียนแทนด้วย $- z$ ) คือ (-a,-b)
ถ้าหาก $z = (a,b) \neq (0,0)$ อินเวอร์สการคูณของ $z$ (เขียนแทนด้วย $z - 1$ ) คือ $\left( \frac{a}{a^2 + b^2}, \frac{-b}{a^2 + b^2} \right)$

จำนวนเชิงซ้อนในฐานะปริภูมิเวกเตอร์และฟีลด์ต่อเติม

อนึ่ง เราอาจมองเซตของจำนวนเชิงซ้อนเป็นปริภูมิเวกเตอร์สองมิติบนเซตของจำนวนจริง เราสามารถใช้การบวกจำนวนเชิงซ้อนแทนการบวกเวกเตอร์ และการคูณด้วยสเกลาร์สามารถนิยามได้ดังต่อไปนี้

$c(a,b) = (ca,cb) = (a,b)c \,$ เมื่อ

c

เป็นจำนวนจริงและ

(a, b)

เป็นจำนวนเชิงซ้อนใดๆ

ด้วยเหตุนี้เราได้ว่าฐานหลักหนึ่งของเซตของจำนวนเชิงซ้อนประกอบด้วยเวกเตอร์

(1,0)

และ

(0,1)

กล่าวคือเราสามารถเขียนจำนวนเชิงซ้อนทุกตัวในรูปของผลรวมเชิงเส้นของเวกเตอร์ทั้งสอง:

$(a,b) = a(1,0) + b(0,1) \,$

ตามความนิยม เรามักแปลความหมายของ

(a,0) = a (1,0)

ว่าเป็นจำนวนจริง

a

(ด้วยเหตุนี้เราจึงกล่าวว่าเซตจำนวนจริงเป็นสับเซตของเซตจำนวนเชิงซ้อน) และมักใช้สัญลักษณ์

i

แทน

(0,1)

จำนวนเชิงซ้อน

(a, b)

จึงเขียนได้อีกแบบหนึ่งว่า

a + b i

ซึ่งเป็นที่นิยมใช้มากกว่าแบบคู่ลำดับ
จากนิยามการคูณจำนวนเชิงซ้อนข้างต้น เราได้ว่า

i 2 = ( - 1,0) = - 1

นั่นคือ

i

เป็นคำตอบของสมการ

x 2 + 1 = 0

ซึ่งไม่สามารถหาคำตอบได้ในเซตของจำนวนจริง ดังนั้น เซตของจำนวนเชิงซ้อนจึงเป็นฟีลด์ต่อเติม (field extension) ของเซตของจำนวนจริงโดยการเพิ่มรากของพหุนาม

x 2 + 1

อีกนัยหนึ่ง เซตของจำนวนเชิงซ้อนคือริงผลหาร (quotient ring) ของริงพหุนาม $\mathbb{R}[x]$ กับไอดีล

(x 2 + 1)

เขียนเป็นประโยคสัญลักษณ์ได้ว่า

$\mathbb{C} = \mathbb{R}[x]/(x^2+1)$

สัญลักษณ์และคำศัพท์ที่เกี่ยวข้อง

ส่วนจริงและส่วนจินตภาพ

ถ้า $z = a+bi \,$ เราเรียก

a

ว่า ส่วนจริง ของ

z

เขียนแทนด้วยสัญลักษณ์ $\Re(z)$ และเราเรียก

b

ว่า ส่วนจินตภาพ ของ

z

เขียนแทนด้วยสัญลักษณ์ $\Im(z)$ เราเรียกจำนวนเชิงซ้อนที่มีส่วนจริงเป็น 0 และส่วนจินตภาพไม่เป็น 0 ว่าจำนวนจินตภาพ (imaginary number)

สังยุคเชิงซ้อน

ถ้า $z=a+bi\,$ เป็นจำนวนเชิงซ้อน สังยุคของ

z

คือ $a-bi\,$ เราเขียนแทนสังยุคของ

z

ด้วย $\bar{z}$ สังยุคของจำนวนเชิงซ้อนมีสมบัติสำคัญๆ ดังต่อไปนี้

$\overline{z_{1}+z_{2}}=\bar{z}_{1}+\bar{z}_{2}$
$\overline{z_{1}z_{2}}=\bar{z}_{1}\bar{z}_{2}$
$z + \bar{z} = 2\Re(z)$
$z - \bar{z} = 2\Im(z)$

เมื่อ

z

z 1

z 2

เป็นจำนวนเชิงซ้อนใดๆ

ขนาดของจำนวนเชิงซ้อน

ขนาดของจำนวนเชิงซ้อน $z=a+bi \,$ เขียนแทนด้วย

| z |

คือจำนวนจริงบวก $\sqrt{a^2 + b^2}$ เราอาจแปลความหมายของขนาดของจำนวนเชิงซ้อนได้ว่าเป็นความยาวของเส้นตรงที่ลากจากจุด (0,0) ไปยังจุด (a,b) บนระนาบคาร์ทีเชียน ขนาดของจำนวนเชิงซ้อนมีสมบัติสำคัญๆ ดังต่อไปนี้

$\left|z\right\vert=\left|\bar z\right\vert$
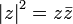
$\left|z\right\vert^2=z \bar{z}$
$\left|z_1z_2\right\vert=\left|z_1\right\vert\left|z_2\right\vert$
$\left|z_1+z_2\right\vert\le\;\left|z_1\right\vert+\left|z_2\right\vert$ (อสมการสามเหลี่ยม)
$\left|z_1-z_2\right\vert\ge\;\big|\left|z_1\right\vert-\left|z_2\right\vert\big|$
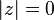$\left|z\right\vert=0$ ก็ต่อเมื่อ $z=0\,$

เมื่อ

z

z 1

, และ

z 2

เป็นจำนวนเชิงซ้อนใดๆ จากสมบัติข้อที่สองและการแทนจำนวนจริง

a

ด้วยจำนวนเชิงซ้อน

(a,0)

ทำให้เราได้ว่าถ้า $z \neq 0$

$z^{-1} = \frac{\bar{z}}{|z|^2}$

ระนาบเชิงซ้อน

เรายังสามารถมองจำนวนเชิงซ้อนเป็นจุดหรือเวกเตอร์บนระนาบคาร์ทีเซียนสองมิติ และมักจะเรียกระนาบนี้ว่าระนาบเชิงซ้อน (complex plane) หรือผังของอาร์กานด์ ตามชื่อของ ชอง-โรแบร์ต อาร์กานด์ ผู้ค้นพบ
พิกัดคาร์ทีเซียนของจำนวนเชิงซ้อน $z = a+bi \,$ คือ

(a, b)

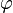ในขณะที่พิกัดเชิงขั้วคิอ $(r,\varphi) \,$ เมื่อ

r = | z |

และ $\varphi \,$ เป็นมุมที่เวกเตอร์

(a, b)

ทำกับแกน

x

ในหน่วยเรเดียน เราเรียก 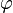$\varphi \,$ ว่า อาร์กิวเมนต์ของ

z

และเขียนแทนด้วยสัญลักษณ์

arg(z)

สังเกตว่าจำนวนเชิงซ้อนที่มีอาร์กิวเมนต์ต่างกันเท่ากับผลคูณของจำนวนเต็มกับ

2π

จะมีค่าเท่ากัน
สูตรของออยเลอร์ช่วยแสดงความสัมพันธ์ระหว่างพิกัดคาร์ทีเซียนและพิกัดเชิงขั้ว อีกทั้งยังช่วยให้เราสามารถเขียนจำนวนเชิงซ้อนได้อีกรูปแบบหนึ่งดังต่อไปนี้

$z = a+bi = r(\cos \varphi + i \sin \varphi) = re^{i\varphi}\,$

และเรายังสามารถพิสูจน์ได้ว่า

$r_1 e^{i\varphi_1} \cdot r_2 e^{i\varphi_2} = r_1r_2e^{i(\varphi_1 + \varphi_2)} = r_1r_2(\cos (\varphi_1+\varphi_2) + i\sin(\varphi_1+\varphi_2))$

และ

$\frac{r_1 e^{i\varphi_1}}{r_2 e^{i\phi_2}} = \frac{r_1}{r_2}e^{i(\varphi_1 - \varphi_2)} = \frac{r_1}{r_2}(\cos (\varphi_1-\varphi_2) + i\sin(\varphi_1-\varphi_2))$

เมื่อ $r_2 \neq 0$ ด้วยเหตุนี้เราจึงสามารถมองการคูณจำนวนเชิงซ้อนตัวหนึ่งๆ ว่าเป็นการหมุนและการยืด (หรือหด) เวกเตอร์ด้วยอาร์กิวเมนต์และขนาดของจำนวนเชิงซ้อนตัวนั้นตามลำดับ
การคูณด้วย

i = e i π / 2

จึงสมมูลกับการหมุนเวกเตอร์ 90 องศาทวนเข็มนาฬิกา สมการ ฉะนั้นเราสามารถเข้าใจความหมายของสมการ

i 2 = - 1

ได้อีกนัยหนึ่งว่า "การหมุน 90 องศาสองครั้งมีค่าเท่ากับการหมุน 180 องศา" หรือ "เมื่อหมุนเวกเตอร์

(0,1)

ไป 90 องศา ผลลัพธ์ที่ได้คือเวกเตอร์ (-1,0)"

สมบัติต่างๆ

การเรียงลำดับ

$\mathbb{C}$ ไม่เป็นฟีลด์อันดับ กล่าวคือเราไม่สามารถเรียงลำดับจำนวนเชิงซ้อนโดยที่การเรียงลำดับนั้นสอดคล้องกับการบวกและการคูณจำนวนเชิงซ้อนได้เลย

ปริภูมิเวกเตอร์

อย่างที่ได้กล่าวไว้ข้างต้น $\mathbb{C}$ เป็นปริภูมิเวกเตอร์สองมิติบน $\mathbb{R}$ เราได้ว่าการแปลงเชิงเส้นบน $\mathbb{R}$ ( $\mathbb{R}$ -linear map) ทุกตัวจะสามารถเขียนได้ในรูป

$f(z) = az + b\bar{z}$

เมื่อ

a

และ

b

เป็นจำนวนเชิงซ้อนใดๆ เราได้ว่าฟังก์ชัน

f 1 (z) = a (z)

เป็นการหมุนและการยืดเวกเตอร์ ส่วนฟังก์ชัน $f_2(z) = b\bar{z}$ นั้นประกอบด้วยการหมุน การพลิก และการยืดเวกเตอร์ในฟังก์ชันเดียว สังเกตว่า

f 1

เท่านั้นที่เป็นการแปลงเชิงเส้นบน $\mathbb{C}$ และเป็นฟังก์ชันโฮโลมอร์ฟิก เราสามารถหาอนุพันธ์ของ

f 2

ได้ในเซตของจำนวนจริง แต่อนุพันธ์นั้นไม่สอดคล้องกับสมการโคชี-รีมันน์

สมบัติเชิงพีชคณิต

$\mathbb{C}$ (หรือฟีลด์อื่นที่สมสัณฐานกับ

C

) จะมีลักษณะจำเพาะสามประการ ดังนี้

มีแคแรกเทอริสติก 0
มีดีกรีอดิศัยเมื่อเทียบกับฟีลด์เฉพาะใดๆ เท่ากับขนาดของเซตจำนวนจริง
มีสมบัติปิดเชิงพีชคณิต (ดู ทฤษฎีบทมูลฐานของพีชคณิต)

ด้วยเหตุนี้ $\mathbb{C}$ จึงมีฟีลด์ย่อย แท้ที่สมสัณฐานกับตัวมันเองอยู่เป็นจำนวนมาก นอกจากนี้กาลอยด์กรุปของ $\mathbb{C}$ บนเชตของจำนวนตรรกยะมีขนาดเท่ากับเซตกำลังของเซตของจำนวนจริง

noojennaka

วันพุธที่ 25 มกราคม พ.ศ. 2555

จำนวนเชิงซ้อน

ฟีลด์ของจำนวนเชิงซ้อน

จำนวนเชิงซ้อนในฐานะปริภูมิเวกเตอร์และฟีลด์ต่อเติม

สัญลักษณ์และคำศัพท์ที่เกี่ยวข้อง

ส่วนจริงและส่วนจินตภาพ

สังยุคเชิงซ้อน

ขนาดของจำนวนเชิงซ้อน

ระนาบเชิงซ้อน

สมบัติต่างๆ

การเรียงลำดับ

ปริภูมิเวกเตอร์

สมบัติเชิงพีชคณิต

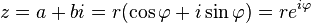
ไม่มีความคิดเห็น:

แสดงความคิดเห็น